How To Draw Mo Energy Diagram

Chapter 8. Advanced Theories of Covalent Bonding

viii.4 Molecular Orbital Theory

Learning Objectives

By the end of this section, y'all will exist able to:

• Outline the basic quantum-mechanical approach to deriving molecular orbitals from atomic orbitals
• Describe traits of bonding and antibonding molecular orbitals
• Calculate bond orders based on molecular electron configurations
• Write molecular electron configurations for first- and second-row diatomic molecules
• Relate these electron configurations to the molecules' stabilities and magnetic properties

For almost every covalent molecule that exists, we tin now describe the Lewis structure, predict the electron-pair geometry, predict the molecular geometry, and come up close to predicting bond angles. However, i of the most important molecules we know, the oxygen molecule O₂, presents a problem with respect to its Lewis construction. We would write the following Lewis structure for O₂:

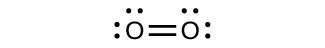
This electronic construction adheres to all the rules governing Lewis theory. There is an O=O double bond, and each oxygen atom has 8 electrons around information technology. Nevertheless, this picture is at odds with the magnetic behavior of oxygen. By itself, O₂ is not magnetic, but it is attracted to magnetic fields. Thus, when nosotros pour liquid oxygen past a potent magnet, it collects between the poles of the magnet and defies gravity, as in Figure one in Chapter 8 Introduction. Such attraction to a magnetic field is chosen paramagnetism, and it arises in molecules that have unpaired electrons. And yet, the Lewis structure of O_ii indicates that all electrons are paired. How do nosotros business relationship for this discrepancy?

Magnetic susceptibility measures the force experienced by a substance in a magnetic field. When nosotros compare the weight of a sample to the weight measured in a magnetic field (Figure 1), paramagnetic samples that are attracted to the magnet volition announced heavier because of the force exerted by the magnetic field. We can calculate the number of unpaired electrons based on the increment in weight.

Figure 1. A Gouy balance compares the mass of a sample in the presence of a magnetic field with the mass with the electromagnet turned off to decide the number of unpaired electrons in a sample.

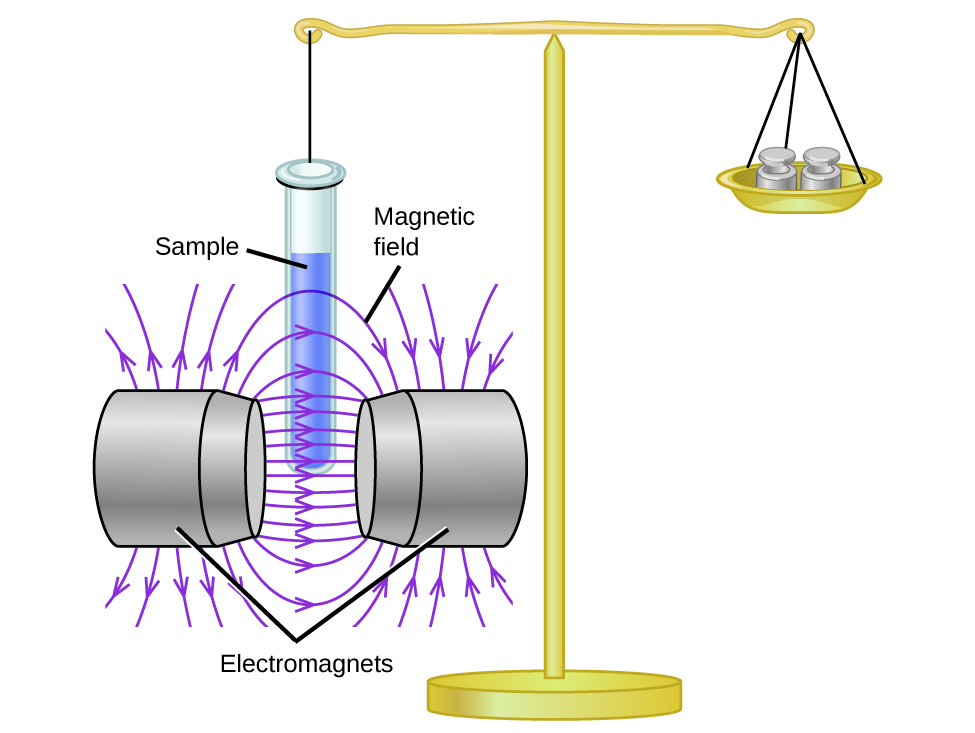
Experiments show that each O₂ molecule has two unpaired electrons. The Lewis-structure model does not predict the presence of these two unpaired electrons. Different oxygen, the apparent weight of most molecules decreases slightly in the presence of an inhomogeneous magnetic field. Materials in which all of the electrons are paired are diamagnetic and weakly repel a magnetic field. Paramagnetic and diamagnetic materials do not human activity as permanent magnets. Only in the presence of an applied magnetic field practice they demonstrate attraction or repulsion.

H2o, similar most molecules, contains all paired electrons. Living things comprise a large percentage of water, and then they demonstrate diamagnetic behavior. If you place a frog near a sufficiently large magnet, it volition levitate. You lot can encounter videos of diamagnetic floating frogs, strawberries, and more.

Molecular orbital theory (MO theory) provides an caption of chemic bonding that accounts for the paramagnetism of the oxygen molecule. It besides explains the bonding in a number of other molecules, such every bit violations of the octet rule and more molecules with more complicated bonding (beyond the scope of this text) that are difficult to describe with Lewis structures. Additionally, it provides a model for describing the energies of electrons in a molecule and the probable location of these electrons. Unlike valence bond theory, which uses hybrid orbitals that are assigned to ane specific atom, MO theory uses the combination of atomic orbitals to yield molecular orbitals that are delocalized over the entire molecule rather than being localized on its elective atoms. MO theory likewise helps us understand why some substances are electrical conductors, others are semiconductors, and even so others are insulators. Table 2 summarizes the main points of the ii complementary bonding theories. Both theories provide dissimilar, useful ways of describing molecular construction.

Valence Bond Theory	Molecular Orbital Theory
considers bonds as localized between ane pair of atoms	considers electrons delocalized throughout the entire molecule
creates bonds from overlap of diminutive orbitals (s, p, d…) and hybrid orbitals (sp, sp 2, sp 3…)	combines atomic orbitals to grade molecular orbitals (σ, σ*, π, π*)
forms σ or π bonds	creates bonding and antibonding interactions based on which orbitals are filled
predicts molecular shape based on the number of regions of electron density	predicts the arrangement of electrons in molecules
needs multiple structures to draw resonance
Table two. Comparison of Bonding Theories

Molecular orbital theory describes the distribution of electrons in molecules in much the same manner that the distribution of electrons in atoms is described using atomic orbitals. Using breakthrough mechanics, the beliefs of an electron in a molecule is still described by a wave function, Ψ, analogous to the behavior in an atom. Only like electrons effectually isolated atoms, electrons effectually atoms in molecules are limited to discrete (quantized) energies. The region of infinite in which a valence electron in a molecule is likely to be found is called a molecular orbital (Ψ ²). Similar an atomic orbital, a molecular orbital is full when it contains 2 electrons with contrary spin.

We volition consider the molecular orbitals in molecules composed of two identical atoms (H_two or Cl₂, for example). Such molecules are called homonuclear diatomic molecules. In these diatomic molecules, several types of molecular orbitals occur.

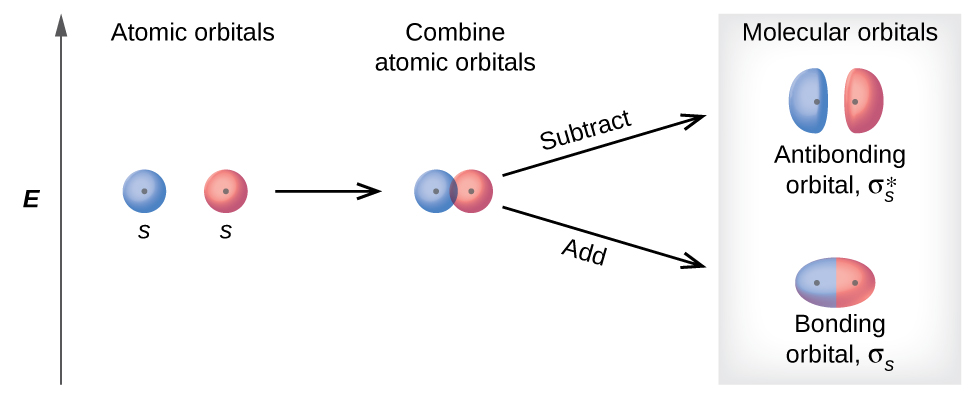
The mathematical process of combining atomic orbitals to generate molecular orbitals is called the linear combination of atomic orbitals (LCAO). The wave function describes the wavelike backdrop of an electron. Molecular orbitals are combinations of atomic orbital moving ridge functions. Combining waves can lead to constructive interference, in which peaks line upwardly with peaks, or destructive interference, in which peaks line upward with troughs (Figure 2). In orbitals, the waves are iii dimensional, and they combine with in-stage waves producing regions with a higher probability of electron density and out-of-phase waves producing nodes, or regions of no electron density.

Figure two. (a) When in-phase waves combine, effective interference produces a moving ridge with greater amplitude. (b) When out-of-phase waves combine, subversive interference produces a moving ridge with less (or no) aamplitude.

In that location are 2 types of molecular orbitals that tin can form from the overlap of two atomic s orbitals on adjacent atoms. The two types are illustrated in Figure 3. The in-phase combination produces a lower energy σ _south molecular orbital (read as "sigma-s") in which near of the electron density is directly between the nuclei. The out-of-phase addition (which can as well be thought of as subtracting the wave functions) produces a higher free energy [latex]\pmb \sigma^*_s[/latex]molecular orbital (read as "sigma-s-star") molecular orbital in which there is a node between the nuclei. The asterisk signifies that the orbital is an antibonding orbital. Electrons in a σ _s orbital are attracted by both nuclei at the same time and are more stable (of lower free energy) than they would be in the isolated atoms. Adding electrons to these orbitals creates a force that holds the 2 nuclei together, and then nosotros call these orbitals bonding orbitals. Electrons in the [latex]\sigma^*_s[/latex] orbitals are located well away from the region between the two nuclei. The attractive force between the nuclei and these electrons pulls the two nuclei autonomously. Hence, these orbitals are called antibonding orbitals. Electrons fill the lower-energy bonding orbital before the college-energy antibonding orbital, just as they fill up lower-energy atomic orbitals before they fill higher-energy atomic orbitals.

Effigy 3. Sigma (σ) and sigma-star (σ*) molecular orbitals are formed by the combination of 2 s diminutive orbitals. The plus (+) signs bespeak the locations of nuclei.

Y'all tin watch animations visualizing the calculated atomic orbitals combining to form diverse molecular orbitals at the Orbitron website.

In p orbitals, the wave function gives ascent to two lobes with opposite phases, analogous to how a two-dimensional moving ridge has both parts above and below the boilerplate. We betoken the phases past shading the orbital lobes different colors. When orbital lobes of the same phase overlap, constructive wave interference increases the electron density. When regions of contrary stage overlap, the destructive moving ridge interference decreases electron density and creates nodes. When p orbitals overlap finish to cease, they create σ and σ* orbitals (Figure 4). If two atoms are located along the x-axis in a Cartesian coordinate system, the two p_x orbitals overlap end to end and form σ _px (bonding) and [latex]\sigma^*_{px}[/latex] (antibonding) (read equally "sigma-p-x" and "sigma-p-x star," respectively). Just as with s-orbital overlap, the asterisk indicates the orbital with a node between the nuclei, which is a college-free energy, antibonding orbital.

Figure four. Combining moving ridge functions of two p atomic orbitals along the internuclear centrality creates two molecular orbitals, σ _p and σ* _p .

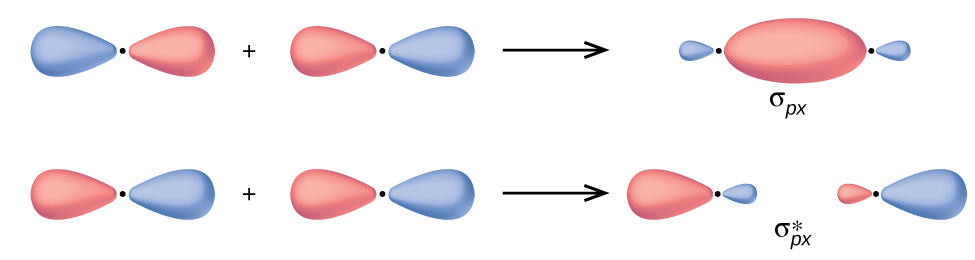
The side-by-side overlap of 2 p orbitals gives rise to a pi (π) bonding molecular orbital and a π* antibonding molecular orbital, as shown in Figure 5. In valence bond theory, nosotros describe π bonds as containing a nodal aeroplane containing the internuclear axis and perpendicular to the lobes of the p orbitals, with electron density on either side of the node. In molecular orbital theory, we depict the π orbital past this same shape, and a π bail exists when this orbital contains electrons. Electrons in this orbital interact with both nuclei and help hold the ii atoms together, making it a bonding orbital. For the out-of-phase combination, there are ii nodal planes created, ane along the internuclear axis and a perpendicular one betwixt the nuclei.

Figure 5. Side-past-side overlap of each two p orbitals results in the germination of two π molecular orbitals. Combining the out-of-stage orbitals results in an antibonding molecular orbital with two nodes. I contains the internuclear centrality, and i is perpendicular to the axis. Combining the in-phase orbitals results in a bonding orbital. There is a node (bluish) containing the internuclear centrality with the two lobes of the orbital located above and beneath this node.

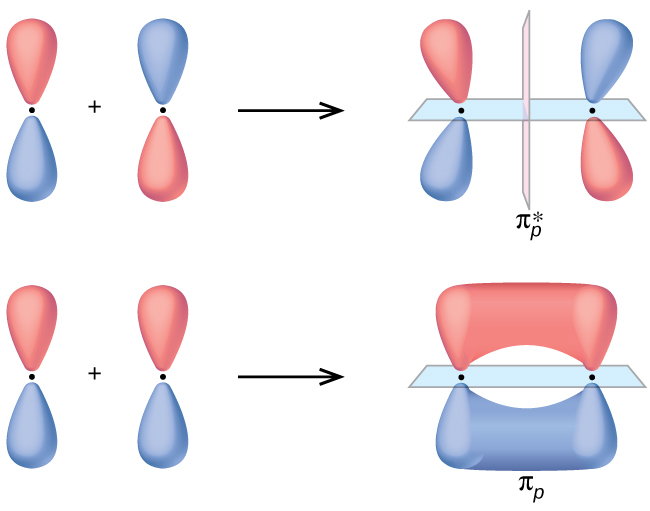
In the molecular orbitals of diatomic molecules, each cantlet also has two sets of p orbitals oriented side by side (p_y and p_z ), and then these four diminutive orbitals combine pairwise to create 2 π orbitals and two π* orbitals. The π _py and [latex]\pi^*_{py}[/latex] orbitals are oriented at right angles to the π _pz and [latex]\pi^*_{pz}[/latex] orbitals. Except for their orientation, the π _py and π _pz orbitals are identical and have the aforementioned energy; they are degenerate orbitals. The [latex]\pi^*_{py}[/latex] and [latex]\pi^*_{px}[/latex] antibonding orbitals are likewise degenerate and identical except for their orientation. A total of six molecular orbitals results from the combination of the half dozen diminutive p orbitals in two atoms: σ _px and [latex]\sigma^*_{px}[/latex], π _py and [latex]\pi^*_{py}[/latex], π _pz and [latex]\pi^*_{pz}[/latex].

Example one

Molecular Orbitals
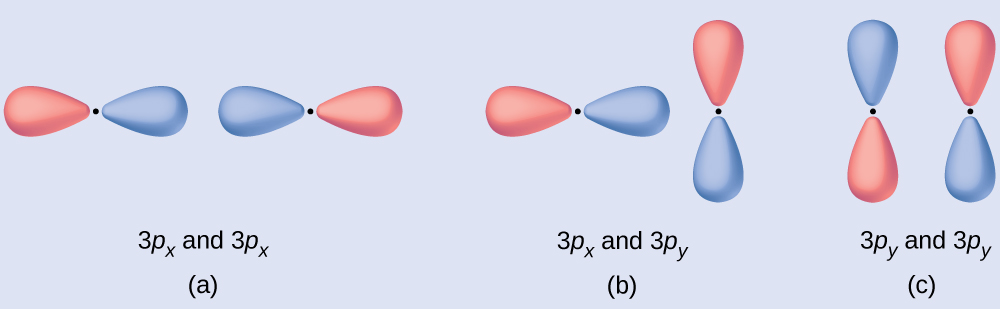
Predict what type (if any) of molecular orbital would issue from calculation the wave functions so each pair of orbitals shown overlap. The orbitals are all similar in energy.

Solution
(a) is an in-phase combination, resulting in a σ_threep orbital

(b) will not result in a new orbital considering the in-phase component (bottom) and out-of-stage component (tiptop) abolish out. Simply orbitals with the right alignment tin combine.

(c) is an out-of-stage combination, resulting in a [latex]\pi^*_{3p}[/latex] orbital.

Check Your Learning
Characterization the molecular orbital shown as σ or π, bonding or antibonding and betoken where the node occurs.

Answer:

The orbital is located along the internuclear axis, then it is a σ orbital. In that location is a node bisecting the internuclear centrality, then information technology is an antibonding orbital.

Walter Kohn: Nobel Laureate

Walter Kohn (Effigy 6) is a theoretical physicist who studies the electronic structure of solids. His work combines the principles of quantum mechanics with avant-garde mathematical techniques. This technique, chosen density functional theory, makes it possible to compute properties of molecular orbitals, including their shape and energies. Kohn and mathematician John Pople were awarded the Nobel Prize in Chemistry in 1998 for their contributions to our understanding of electronic structure. Kohn as well made significant contributions to the physics of semiconductors.

Figure 6. Walter Kohn developed methods to describe molecular orbitals. (credit: image courtesy of Walter Kohn)

Kohn'due south biography has been remarkable outside the realm of physical chemistry likewise. He was born in Austria, and during World War 2 he was function of the Kindertransport program that rescued x,000 children from the Nazi regime. His summertime jobs included discovering gold deposits in Canada and helping Polaroid explicate how its instant picture worked. Although he is at present an emeritus professor, he is still actively working on projects involving global warming and renewable energy.

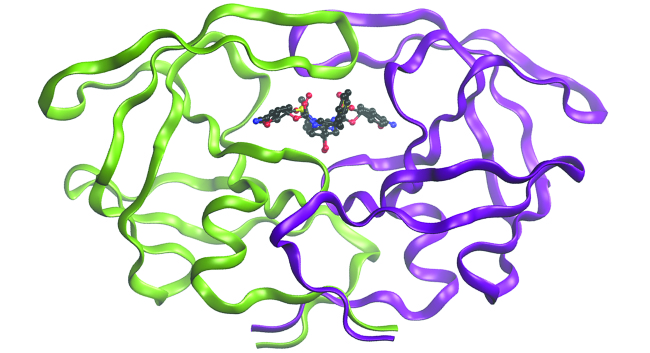
Computational Chemistry in Drug Pattern

While the descriptions of bonding described in this chapter involve many theoretical concepts, they also have many practical, real-world applications. For case, drug design is an of import field that uses our understanding of chemical bonding to develop pharmaceuticals. This interdisciplinary area of written report uses biology (understanding diseases and how they operate) to identify specific targets, such equally a binding site that is involved in a disease pathway. By modeling the structures of the binding site and potential drugs, computational chemists can predict which structures can fit together and how effectively they will bind (see Effigy seven). Thousands of potential candidates can be narrowed down to a few of the well-nigh promising candidates. These candidate molecules are then advisedly tested to determine side effects, how finer they tin exist transported through the body, and other factors. Dozens of of import new pharmaceuticals take been discovered with the aid of computational chemistry, and new research projects are underway.

Figure 7. The molecule shown, HIV-one protease, is an important target for pharmaceutical research. By designing molecules that bind to this protein, scientists are able to drastically inhibit the progress of the illness.

Molecular Orbital Energy Diagrams

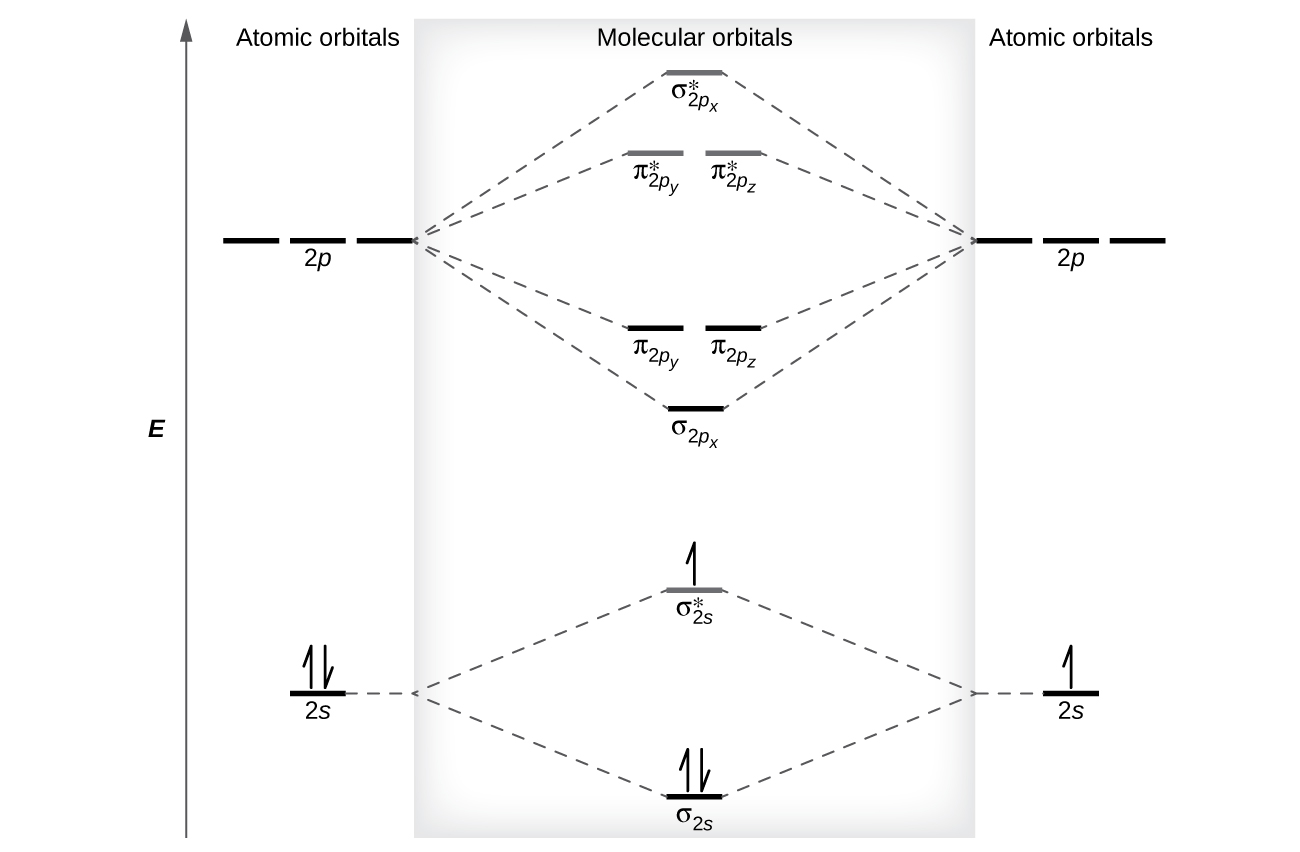
The relative energy levels of diminutive and molecular orbitals are typically shown in a molecular orbital diagram (Effigy 8). For a diatomic molecule, the atomic orbitals of i atom are shown on the left, and those of the other atom are shown on the right. Each horizontal line represents one orbital that can concord two electrons. The molecular orbitals formed past the combination of the atomic orbitals are shown in the center. Dashed lines show which of the diminutive orbitals combine to class the molecular orbitals. For each pair of atomic orbitals that combine, i lower-energy (bonding) molecular orbital and one higher-energy (antibonding) orbital event. Thus nosotros can run into that combining the six 2p diminutive orbitals results in three bonding orbitals (ane σ and ii π) and iii antibonding orbitals (ane σ* and ii π*).

We predict the distribution of electrons in these molecular orbitals by filling the orbitals in the same manner that we make full atomic orbitals, past the Aufbau principle. Lower-energy orbitals fill showtime, electrons spread out among degenerate orbitals before pairing, and each orbital tin hold a maximum of 2 electrons with opposite spins (Figure 8). Just as nosotros write electron configurations for atoms, we tin can write the molecular electronic configuration by list the orbitals with superscripts indicating the number of electrons present. For clarity, we place parentheses around molecular orbitals with the same energy. In this case, each orbital is at a different free energy, so parentheses separate each orbital. Thus nosotros would look a diatomic molecule or ion containing vii electrons (such every bit Be₂ ⁺) would take the molecular electron configuration [latex](\sigma_{1s})^2[/latex] [latex](\sigma^*_{1s})^two[/latex] [latex](\sigma_{2s})^2[/latex] [latex](\sigma^*_{2s})^i[/latex]. It is common to omit the core electrons from molecular orbital diagrams and configurations and include only the valence electrons.

Figure viii. This is the molecular orbital diagram for the homonuclear diatomic Be₂ ⁺, showing the molecular orbitals of the valence shell just. The molecular orbitals are filled in the same fashion as atomic orbitals, using the Aufbau principle and Hund'southward rule.

Bond Order

The filled molecular orbital diagram shows the number of electrons in both bonding and antibonding molecular orbitals. The net contribution of the electrons to the bail strength of a molecule is identified by determining the bond guild that results from the filling of the molecular orbitals by electrons.

When using Lewis structures to draw the distribution of electrons in molecules, we define bond guild as the number of bonding pairs of electrons between two atoms. Thus a single bond has a bond order of 1, a double bond has a bond gild of 2, and a triple bond has a bond gild of 3. We ascertain bail order differently when we employ the molecular orbital clarification of the distribution of electrons, but the resulting bail order is usually the same. The MO technique is more accurate and can handle cases when the Lewis structure method fails, but both methods describe the same phenomenon.

In the molecular orbital model, an electron contributes to a bonding interaction if it occupies a bonding orbital and it contributes to an antibonding interaction if it occupies an antibonding orbital. The bond lodge is calculated by subtracting the destabilizing (antibonding) electrons from the stabilizing (bonding) electrons. Since a bond consists of two electrons, we divide by two to get the bond order. We tin can determine bail social club with the post-obit equation:

[latex]\text{bond lodge} = \frac{(\text{number of bonding electrons}) - (\text{number of antibonding electrons})}{two}[/latex]

The order of a covalent bond is a guide to its strength; a bond between two given atoms becomes stronger as the bond club increases (Table 1 in Affiliate 8.1 Valence Bond Theory). If the distribution of electrons in the molecular orbitals between 2 atoms is such that the resulting bond would take a bond club of zero, a stable bond does non grade. We side by side look at some specific examples of MO diagrams and bond orders.

Bonding in Diatomic Molecules

A dihydrogen molecule (H₂) forms from ii hydrogen atoms. When the diminutive orbitals of the ii atoms combine, the electrons occupy the molecular orbital of lowest free energy, the σ_{1due south} bonding orbital. A dihydrogen molecule, H₂, readily forms because the energy of a H₂ molecule is lower than that of 2 H atoms. The σ_1s orbital that contains both electrons is lower in energy than either of the ii 1due south diminutive orbitals.

A molecular orbital can hold 2 electrons, so both electrons in the H₂ molecule are in the σ_{onedue south} bonding orbital; the electron configuration is [latex](\sigma_{1s})^2[/latex]. Nosotros represent this configuration by a molecular orbital energy diagram (Figure 9) in which a single upward arrow indicates i electron in an orbital, and two (upward and downward) arrows indicate ii electrons of reverse spin.

Figure ix. The molecular orbital energy diagram predicts that H₂ will be a stable molecule with lower energy than the separated atoms.

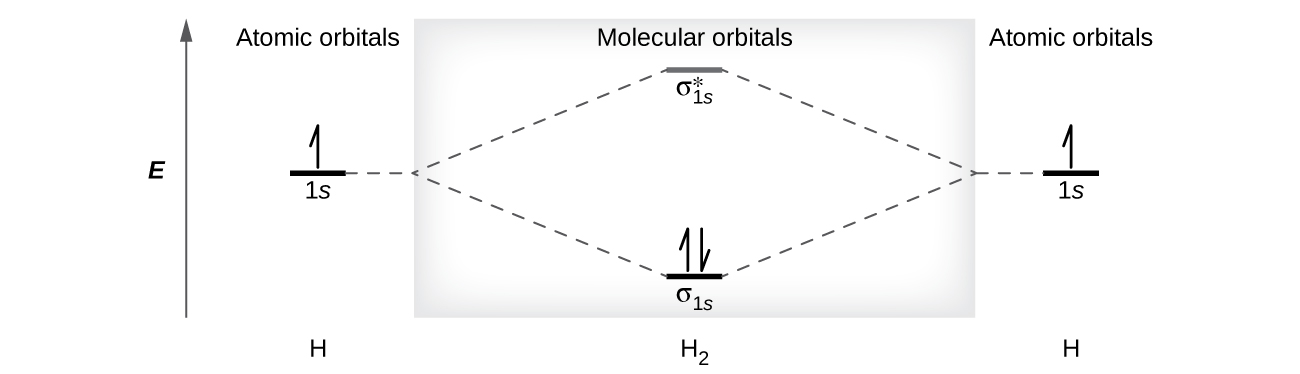
A dihydrogen molecule contains two bonding electrons and no antibonding electrons so we have

[latex]\text{bond order in H}_2 = \frac{(2 - 0)}{two} = ane[/latex]

Considering the bond guild for the H–H bond is equal to 1, the bail is a unmarried bond.

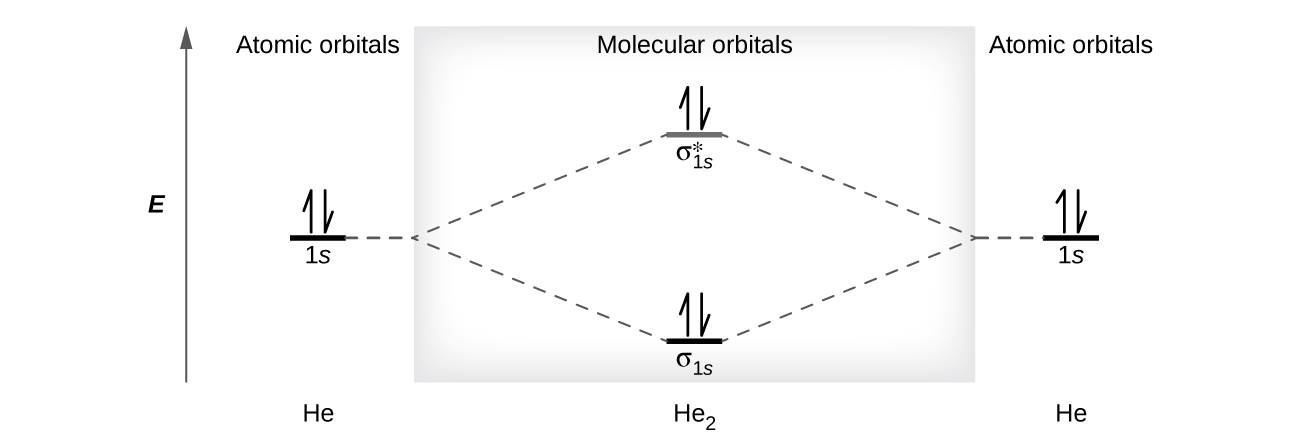
A helium atom has two electrons, both of which are in its 1southward orbital. Two helium atoms do not combine to course a dihelium molecule, He₂, with iv electrons, because the stabilizing effect of the two electrons in the lower-energy bonding orbital would be beginning by the destabilizing event of the ii electrons in the higher-free energy antibonding molecular orbital. Nosotros would write the hypothetical electron configuration of He₂ equally [latex](\sigma_{1s})^2[/latex] [latex](\sigma^*_{1s})^ii[/latex] every bit in Figure x. The internet energy change would be zero, then there is no driving strength for helium atoms to class the diatomic molecule. In fact, helium exists equally discrete atoms rather than as diatomic molecules. The bail lodge in a hypothetical dihelium molecule would be zero.

[latex]\text{bail gild in He}_2 = \frac{(2 - ii)}{2} = 0[/latex]

A bond lodge of nix indicates that no bail is formed between two atoms.

Figure x. The molecular orbital free energy diagram predicts that He₂ volition non exist a stable molecule, since it has equal numbers of bonding and antibonding electrons.

The Diatomic Molecules of the Second Period

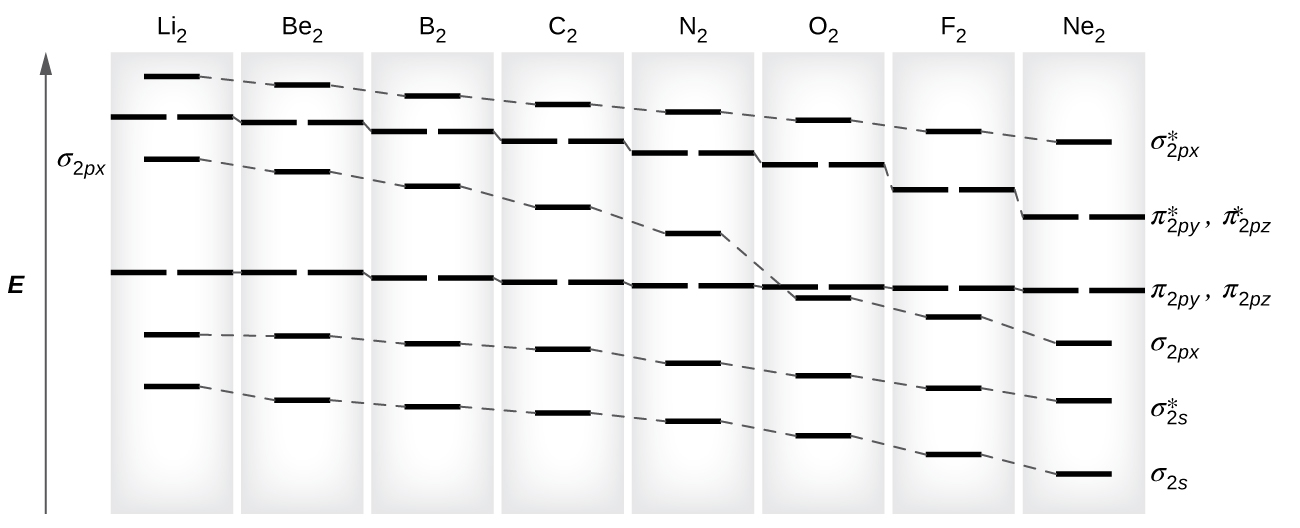
Eight possible homonuclear diatomic molecules might be formed by the atoms of the second period of the periodic table: Li_ii, Be₂, B₂, C₂, N_two, O_ii, F₂, and Ne_two. Even so, we tin can predict that the Be_ii molecule and the Ne₂ molecule would non be stable. We tin run across this by a consideration of the molecular electron configurations (Table 3).

We predict valence molecular orbital electron configurations just equally we predict electron configurations of atoms. Valence electrons are assigned to valence molecular orbitals with the lowest possible energies. Consistent with Hund'south rule, whenever there are two or more degenerate molecular orbitals, electrons fill each orbital of that type singly earlier whatsoever pairing of electrons takes place.

As nosotros saw in valence bond theory, σ bonds are generally more stable than π bonds formed from degenerate atomic orbitals. Similarly, in molecular orbital theory, σ orbitals are usually more stable than π orbitals. Nevertheless, this is not always the example. The MOs for the valence orbitals of the 2d period are shown in Figure 11. Looking at Ne₂ molecular orbitals, we see that the social club is consistent with the generic diagram shown in the previous section. However, for atoms with three or fewer electrons in the p orbitals (Li through N) we observe a different pattern, in which the σ _p orbital is higher in free energy than the π _p gear up. Obtain the molecular orbital diagram for a homonuclear diatomic ion by adding or subtracting electrons from the diagram for the neutral molecule.

Figure eleven. This shows the MO diagrams for each homonuclear diatomic molecule in the 2d period. The orbital energies decrease beyond the period equally the effective nuclear charge increases and atomic radius decreases. Betwixt N₂ and O₂, the club of the orbitals changes.

You tin exercise labeling and filling molecular orbitals with this interactive tutorial from the University of Sydney.

This switch in orbital ordering occurs considering of a miracle called s-p mixing. s-p mixing does not create new orbitals; information technology merely influences the energies of the existing molecular orbitals. The σ_{due south} wavefunction mathematically combines with the σ_p wavefunction, with the result that the σ_s orbital becomes more stable, and the σ_p orbital becomes less stable (Figure 12). Similarly, the antibonding orbitals also undergo southward-p mixing, with the σ_s* becoming more stable and the σ_p* becoming less stable.

Figure 12. Without mixing, the MO pattern occurs as expected, with the σ_p orbital lower in energy than the σ_p orbitals. When due south-p mixing occurs, the orbitals shift as shown, with the σ_p orbital higher in energy than the π_p orbitals.

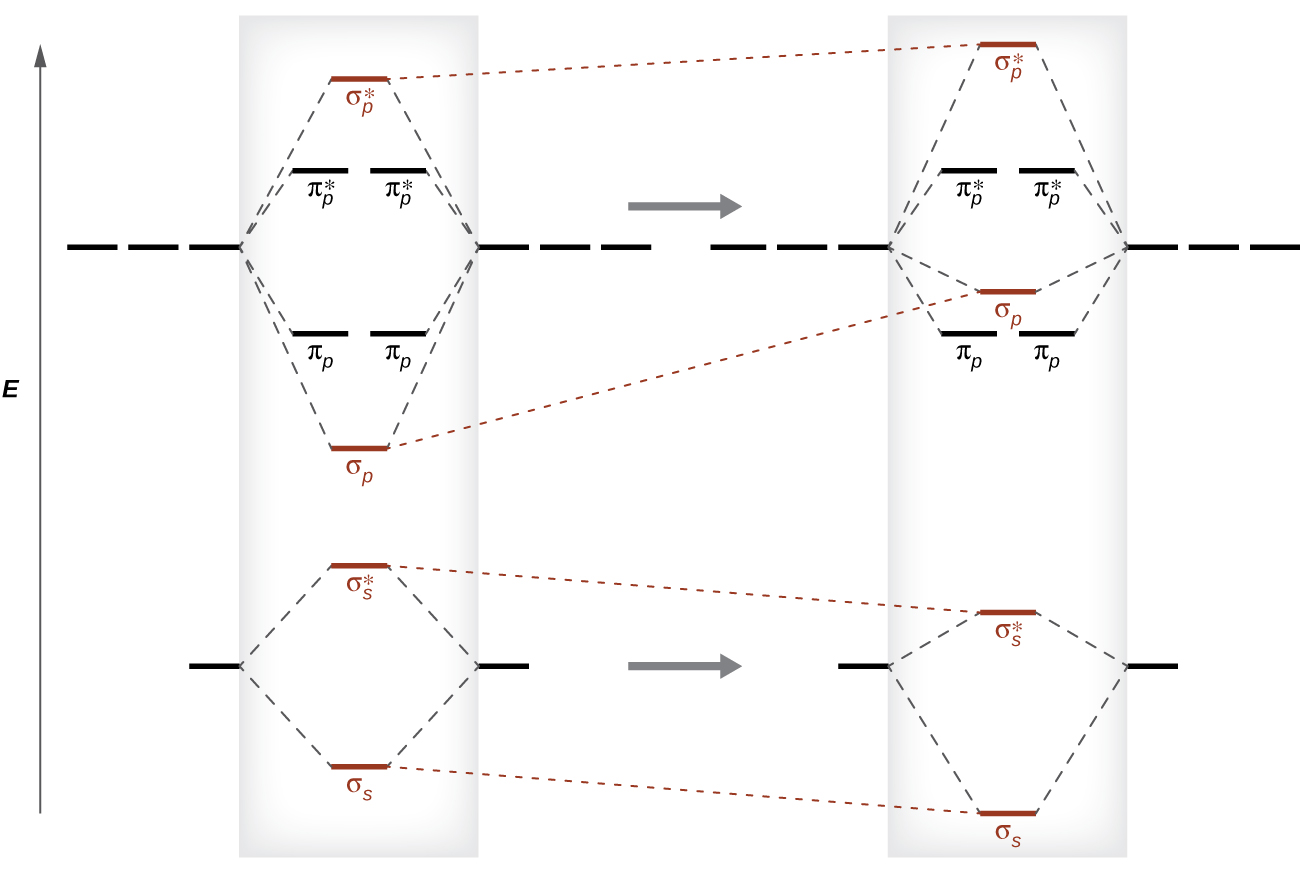
s-p mixing occurs when the s and p orbitals take like energies. When a single p orbital contains a pair of electrons, the human action of pairing the electrons raises the energy of the orbital. Thus the iip orbitals for O, F, and Ne are higher in energy than the 2p orbitals for Li, Be, B, C, and North. Because of this, O₂, F₂, and Northward₂ only take negligible s-p mixing (non sufficient to change the free energy ordering), and their MO diagrams follow the normal design, as shown in Figure 11. All of the other menstruum 2 diatomic molecules do take due south-p mixing, which leads to the design where the σ_p orbital is raised above the π_p prepare.

Using the MO diagrams shown in Effigy xi, we tin add in the electrons and determine the molecular electron configuration and bail order for each of the diatomic molecules. As shown in Table 3, Exist₂ and Ne₂ molecules would have a bail gild of 0, and these molecules do not exist.

Molecule	Electron Configuration	Bond Club
Liii	[latex](\sigma_{2s})^2[/latex]	i
Be2 (unstable)	[latex](\sigma_{2s})^two (\sigma^*_{2s})^2[/latex]	0
B2	[latex](\sigma_{2s})^2 (\sigma^*_{2s})^ii (\pi_{2py}, \pi_{2pz})^2[/latex]	1
C2	[latex](\sigma_{2s})^2 (\sigma^*_{2s})^2 (\pi_{2py}, \pi_{2pz})^4[/latex]	two
N2	[latex](\sigma_{2s})^two (\sigma^*_{2s})^two (\pi_{2py}, \pi_{2pz})^iv (\sigma_{2px})^ii[/latex]	3
O2	[latex](\sigma_{2s})^2 (\sigma^*_{2s})^ii (\sigma_{2px})^two (\pi_{2py}, \pi_{2pz})^4 (\pi^*_{2py}, \pi^*_{2pz})^2[/latex]	ii
F2	[latex](\sigma_{2s})^2 (\sigma^*_{2s})^2 (\sigma_{2px})^ii (\pi_{2py}, \pi_{2pz})^4 (\pi^*_{2py}, \pi^*_{2pz})^4[/latex]	1
Ne2 (unstable)	[latex](\sigma_{2s})^2 (\sigma^*_{2s})^2 (\sigma_{2px})^two (\pi_{2py}, \pi_{2pz})^4 (\pi^*_{2py}, \pi^*_{2pz})^4 (\sigma^*_{2px})^2[/latex]	0
Table 3. Electron Configuration and Bail Order for Molecular Orbitals in Homonuclear Diatomic Molecules of Period Ii Elements

The combination of ii lithium atoms to form a lithium molecule, Li₂, is coordinating to the formation of H_ii, but the atomic orbitals involved are the valence 2due south orbitals. Each of the two lithium atoms has 1 valence electron. Hence, we have two valence electrons bachelor for the σ_twos bonding molecular orbital. Considering both valence electrons would be in a bonding orbital, we would predict the Li₂ molecule to be stable. The molecule is, in fact, present in appreciable concentration in lithium vapor at temperatures near the boiling point of the element. All of the other molecules in Table 3 with a bail order greater than nothing are too known.

The O_two molecule has enough electrons to one-half fill the ([latex]\pi^*_{2py}[/latex], [latex]\pi^*_{2pz}[/latex]) level. Nosotros expect the ii electrons that occupy these two degenerate orbitals to be unpaired, and this molecular electronic configuration for O_two is in accord with the fact that the oxygen molecule has 2 unpaired electrons (Effigy fourteen). The presence of two unpaired electrons has proved to be difficult to explain using Lewis structures, but the molecular orbital theory explains it quite well. In fact, the unpaired electrons of the oxygen molecule provide a potent slice of support for the molecular orbital theory.

Ring Theory

When two identical atomic orbitals on unlike atoms combine, two molecular orbitals issue (run into Effigy iii). The bonding orbital is lower in energy than the original diminutive orbitals because the atomic orbitals are in-phase in the molecular orbital. The antibonding orbital is higher in energy than the original diminutive orbitals considering the diminutive orbitals are out-of-phase.

In a solid, like things happen, but on a much larger scale. Remember that even in a pocket-size sample in that location are a huge number of atoms (typically > 10²³ atoms), and therefore a huge number of atomic orbitals that may be combined into molecular orbitals. When Due north valence diminutive orbitals, all of the same energy and each containing i (1) electron, are combined, N/2 (filled) bonding orbitals and N/ii (empty) antibonding orbitals will upshot. Each bonding orbital will evidence an energy lowering as the atomic orbitals are more often than not in-stage, only each of the bonding orbitals will exist a picayune different and take slightly unlike energies. The antibonding orbitals volition show an increase in energy as the atomic orbitals are generally out-of-phase, only each of the antibonding orbitals volition also be a little different and have slightly different energies. The allowed free energy levels for all the bonding orbitals are so close together that they form a ring, called the valence band. Besides, all the antibonding orbitals are very close together and form a ring, called the conduction band. Effigy 13 shows the bands for three of import classes of materials: insulators, semiconductors, and conductors.

Figure xiii. Molecular orbitals in solids are then closely spaced that they are described as bands. The valence band is lower in energy and the conduction band is higher in energy. The type of solid is determined past the size of the "band gap" betwixt the valence and conduction bands. Only a very small amount of energy is required to move electrons from the valance band to the conduction ring in a conductor, and then they conduct electricity well. In an insulator, the band gap is large, so that very few electrons move, and they are poor conductors of electricity. Semiconductors are in betwixt: they conduct electricity meliorate than insulators, merely not likewise as conductors.

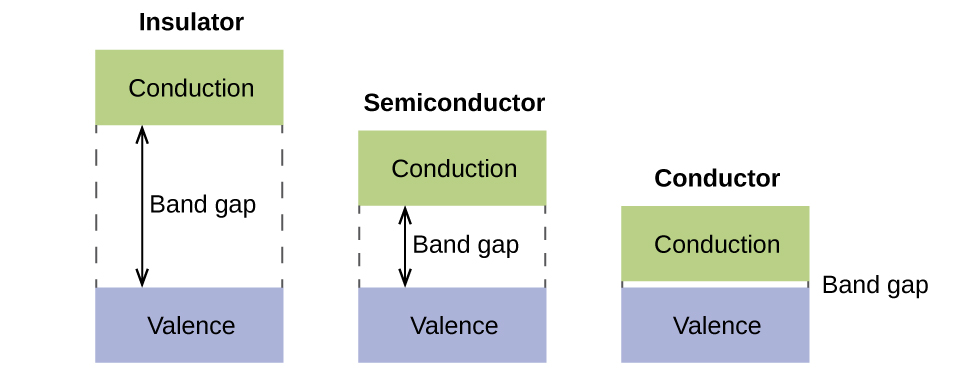
In guild to comport electricity, electrons must move from the filled valence band to the empty conduction band where they can move throughout the solid. The size of the band gap, or the energy difference betwixt the top of the valence band and the bottom of the conduction ring, determines how easy information technology is to motility electrons betwixt the bands. Only a small amount of energy is required in a conductor because the band gap is very pocket-sized. This small energy difference is "easy" to overcome, and then they are good conductors of electricity. In an insulator, the band gap is so "large" that very few electrons move into the conduction ring; as a outcome, insulators are poor conductors of electricity. Semiconductors conduct electricity when "moderate" amounts of energy are provided to move electrons out of the valence band and into the conduction band. Semiconductors, such equally silicon, are found in many electronics.

Semiconductors are used in devices such equally computers, smartphones, and solar cells. Solar cells produce electricity when light provides the energy to move electrons out of the valence band. The electricity that is generated may and so be used to power a light or tool, or information technology can be stored for later use past charging a battery. As of December 2014, up to 46% of the energy in sunlight could be converted into electricity using solar cells.

Instance 2

Molecular Orbital Diagrams, Bond Club, and Number of Unpaired Electrons
Depict the molecular orbital diagram for the oxygen molecule, O₂. From this diagram, summate the bond order for O₂. How does this diagram account for the paramagnetism of O_ii?

Solution

We draw a molecular orbital free energy diagram similar to that shown in Figure 11. Each oxygen atom contributes six electrons, and so the diagram appears equally shown in Effigy 14.

Figure 14. The molecular orbital free energy diagram for O₂ predicts two unpaired electrons.

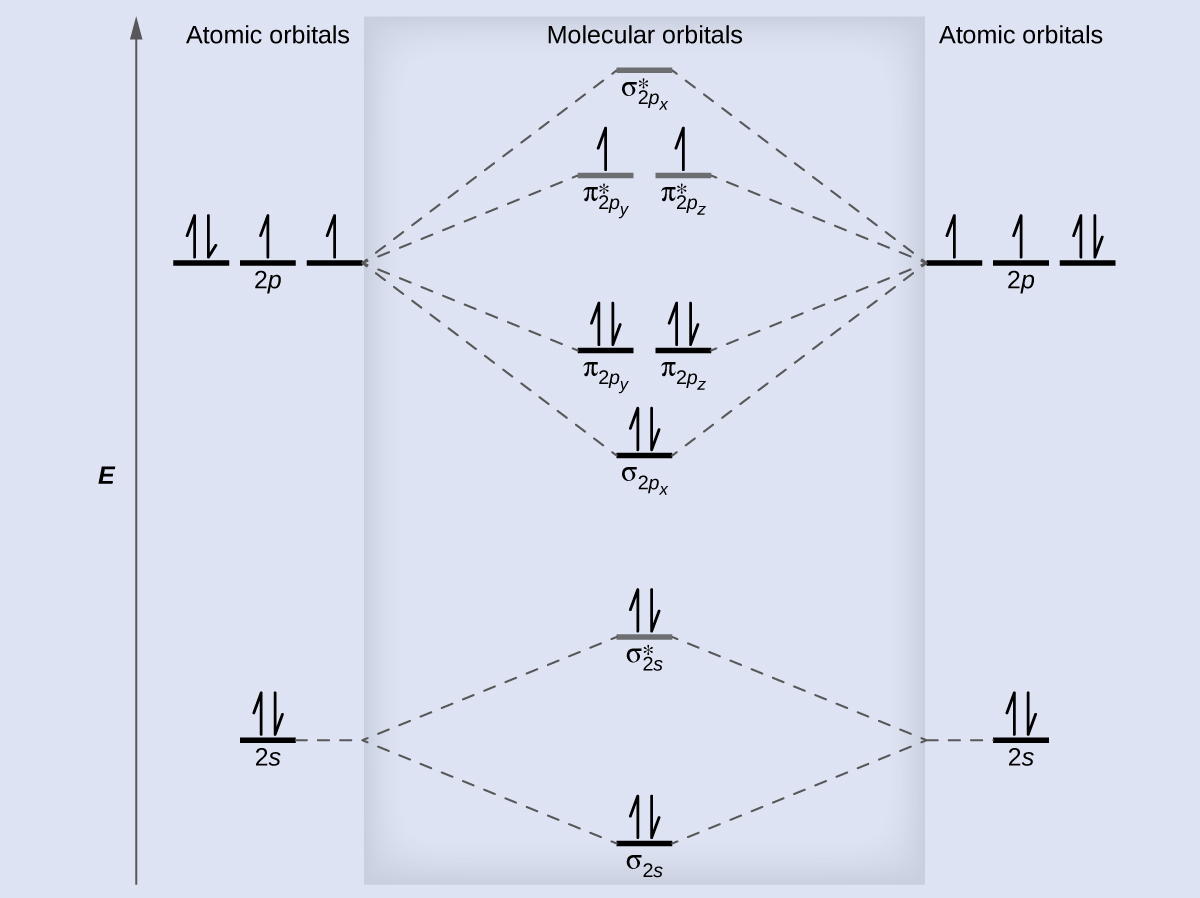
Nosotros calculate the bond order as

[latex]\text{O}_2 = \frac{eight - iv}{2} = 2[/latex]

Oxygen's paramagnetism is explained by the presence of two unpaired electrons in the (π_2py , π_2pz )* molecular orbitals.

Cheque Your Learning

The primary component of air is N₂. From the molecular orbital diagram of Northward₂, predict its bond order and whether it is diamagnetic or paramagnetic.

Answer:

N₂ has a bond order of 3 and is diamagnetic.

Example three

Ion Predictions with MO Diagrams
Give the molecular orbital configuration for the valence electrons in C₂ ⁱⁱ⁻. Will this ion exist stable?

Solution

Looking at the appropriate MO diagram, we meet that the π orbitals are lower in energy than the σ _p orbital. The valence electron configuration for C_two is [latex](\sigma_{2s})^2 (\sigma^*_{2s})^2 (\pi_{2py}, \pi_{2pz})^4[/latex]. Adding two more electrons to generate the C₂ ²⁻ anion volition requite a valence electron configuration of [latex](\sigma_{2s})^2 (\sigma^*_{2s})^2 (\pi_{2py}, \pi_{2pz})^four (\sigma_{2px})^2[/latex]. Since this has six more bonding electrons than antibonding, the bond order will be iii, and the ion should be stable.

Cheque Your Learning

How many unpaired electrons would be present on a Exist_ii ²⁻ ion? Would it be paramagnetic or diamagnetic?

Answer:

two, paramagnetic

Creating molecular orbital diagrams for molecules with more than than two atoms relies on the aforementioned basic ideas as the diatomic examples presented hither. Notwithstanding, with more than atoms, computers are required to summate how the diminutive orbitals combine. See iii-dimensional drawings of the molecular orbitals for C_{half dozen}H₆.

Primal Concepts and Summary

Molecular orbital (MO) theory describes the beliefs of electrons in a molecule in terms of combinations of the atomic wave functions. The resulting molecular orbitals may extend over all the atoms in the molecule. Bonding molecular orbitals are formed by in-phase combinations of atomic wave functions, and electrons in these orbitals stabilize a molecule. Antibonding molecular orbitals issue from out-of-phase combinations of atomic wave functions and electrons in these orbitals brand a molecule less stable. Molecular orbitals located along an internuclear axis are called σ MOs. They tin exist formed from s orbitals or from p orbitals oriented in an end-to-end way. Molecular orbitals formed from p orbitals oriented in a side-by-side way have electron density on contrary sides of the internuclear centrality and are chosen π orbitals.

We can draw the electronic structure of diatomic molecules by applying molecular orbital theory to the valence electrons of the atoms. Electrons fill molecular orbitals following the same rules that apply to filling atomic orbitals; Hund's rule and the Aufbau principle tell the states that lower-energy orbitals will fill first, electrons will spread out before they pair up, and each orbital can agree a maximum of 2 electrons with contrary spins. Materials with unpaired electrons are paramagnetic and attracted to a magnetic field, while those with all-paired electrons are diamagnetic and repelled past a magnetic field. Correctly predicting the magnetic properties of molecules is in reward of molecular orbital theory over Lewis structures and valence bond theory.

Key Equations

• [latex]\text{bond order} = \frac{(\text{number of bonding electron}) - (\text{number of antibonding electrons})}{2}[/latex]

Chemistry End of Chapter Exercises

1. Sketch the distribution of electron density in the bonding and antibonding molecular orbitals formed from ii south orbitals and from two p orbitals.
2. How are the post-obit similar, and how practise they differ?

   (a) σ molecular orbitals and π molecular orbitals

   (b) ψ for an atomic orbital and ψ for a molecular orbital

   (c) bonding orbitals and antibonding orbitals

3. If molecular orbitals are created past combining five atomic orbitals from cantlet A and five atomic orbitals from atom B combine, how many molecular orbitals will issue?
4. Can a molecule with an odd number of electrons ever be diamagnetic? Explain why or why non.
5. Can a molecule with an fifty-fifty number of electrons always be paramagnetic? Explicate why or why not.
6. Why are bonding molecular orbitals lower in free energy than the parent atomic orbitals?
7. Calculate the bail order for an ion with this configuration:

   [latex](\sigma_{2s})^ii (\sigma^*_{2s})^2 (\sigma_{2px})^2 (\pi_{2py} , \pi_{2pz})^iv (\pi^*_{2py} , \pi^*_{2pz})^3[/latex]

8. Explicate why an electron in the bonding molecular orbital in the H₂ molecule has a lower free energy than an electron in the 1s atomic orbital of either of the separated hydrogen atoms.
9. Predict the valence electron molecular orbital configurations for the following, and land whether they volition exist stable or unstable ions.

   (a) Na₂ ^two+

   (b) Mg₂ ^two+

   (c) Al₂ ²⁺

   (d) Si₂ ⁱⁱ⁺

   (due east) P₂ ²⁺

   (f) South₂ ²⁺

   (m) F₂ ⁱⁱ⁺

   (h) Ar₂ ²⁺

10. Decide the bond order of each member of the following groups, and determine which member of each group is predicted past the molecular orbital model to have the strongest bond.

    (a) H_two, H₂ ⁺, H₂ ⁻

    (b) O_ii, O₂ ²⁺, O₂ ²⁻

    (c) Li₂, Exist₂ ⁺, Be₂

    (d) F₂, F₂ ⁺, F_ii ⁻

    (eastward) North_two, North₂ ⁺, Northward_ii ⁻

11. For the first ionization energy for an N_two molecule, what molecular orbital is the electron removed from?
12. Compare the atomic and molecular orbital diagrams to place the member of each of the following pairs that has the highest showtime ionization energy (the most tightly bound electron) in the gas stage:

    (a) H and H₂

    (b) N and N₂

    (c) O and O₂

    (d) C and C_ii

    (east) B and B₂

13. Which of the period 2 homonuclear diatomic molecules are predicted to be paramagnetic?
14. A friend tells you that the 2due south orbital for fluorine starts off at a much lower energy than the 2southward orbital for lithium, so the resulting σ_2south molecular orbital in F₂ is more stable than in Li₂. Practice you agree?
15. True or faux: Boron contains 2southward ²2p ¹ valence electrons, then but one p orbital is needed to form molecular orbitals.
16. What charge would be needed on F_ii to generate an ion with a bond order of 2?
17. Predict whether the MO diagram for S_ii would show southward-p mixing or not.
18. Explain why N₂ ²⁺ is diamagnetic, while O₂ ⁴⁺, which has the same number of valence electrons, is paramagnetic.
19. Using the MO diagrams, predict the bond order for the stronger bail in each pair:

    (a) B₂ or B₂ ⁺

    (b) F_ii or F_two ⁺

    (c) O₂ or O₂ ⁱⁱ⁺

    (d) C_ii ⁺ or C₂ ⁻

Glossary

antibonding orbital

molecular orbital located outside of the region between ii nuclei; electrons in an antibonding orbital destabilize the molecule

bond club

number of pairs of electrons between ii atoms; it tin can exist establish past the number of bonds in a Lewis structure or by the difference betwixt the number of bonding and antibonding electrons divided by ii

bonding orbital

molecular orbital located betwixt two nuclei; electrons in a bonding orbital stabilize a molecule

degenerate orbitals

orbitals that have the same free energy

diamagnetism

phenomenon in which a material is not magnetic itself but is repelled by a magnetic field; it occurs when at that place are but paired electrons present

homonuclear diatomic molecule

molecule consisting of two identical atoms

linear combination of atomic orbitals

technique for combining atomic orbitals to create molecular orbitals

molecular orbital

region of space in which an electron has a high probability of being found in a molecule

molecular orbital diagram

visual representation of the relative energy levels of molecular orbitals

molecular orbital theory

model that describes the beliefs of electrons delocalized throughout a molecule in terms of the combination of diminutive moving ridge functions

paramagnetism

phenomenon in which a textile is non magnetic itself only is attracted to a magnetic field; information technology occurs when in that location are unpaired electrons present

π bonding orbital

molecular orbital formed by side-by-side overlap of atomic orbitals, in which the electron density is institute on opposite sides of the internuclear axis

π* bonding orbital

antibonding molecular orbital formed past out of stage side-by-side overlap of atomic orbitals, in which the electron density is plant on both sides of the internuclear axis, and there is a node between the nuclei

σ bonding orbital

molecular orbital in which the electron density is constitute along the axis of the bond

σ* bonding orbital

antibonding molecular orbital formed by out-of-phase overlap of diminutive orbital along the axis of the bond, generating a node betwixt the nuclei

s-p mixing

change that causes σ _p orbitals to be less stable than π _p orbitals due to the mixing of s and p-based molecular orbitals of similar energies.

Solutions

Answers to Chemistry Stop of Chapter Exercises

2. (a) Similarities: Both are bonding orbitals that can contain a maximum of ii electrons. Differences: σ orbitals are end-to-end combinations of atomic orbitals, whereas π orbitals are formed past side-by-side overlap of orbitals. (b) Similarities: Both are breakthrough-mechanical constructs that represent the probability of finding the electron about the atom or the molecule. Differences: ψ for an atomic orbital describes the behavior of simply ane electron at a time based on the atom. For a molecule, ψ represents a mathematical combination of diminutive orbitals. (c) Similarities: Both are orbitals that tin can contain 2 electrons. Differences: Bonding orbitals result in property two or more atoms together. Antibonding orbitals accept the upshot of destabilizing whatever bonding that has occurred.

4. An odd number of electrons tin never exist paired, regardless of the arrangement of the molecular orbitals. It will ever be paramagnetic.

half dozen. Bonding orbitals have electron density in close proximity to more than one nucleus. The interaction between the bonding positively charged nuclei and negatively charged electrons stabilizes the system.

8. The pairing of the two bonding electrons lowers the energy of the system relative to the energy of the nonbonded electrons.

x. (a) H_ii bail order = 1, H₂ ⁺ bond order = 0.5, H₂ ⁻ bond order = 0.5, strongest bond is H₂; (b) O₂ bond order = two, O_ii ²⁺ bond order = 3; O₂ ^two− bond order = 1, strongest bond is O_two ^two+; (c) Li₂ bond society = ane, Exist₂ ⁺ bond order = 0.5, Exist₂ bail order = 0, strongest bond is Li_two;(d) F₂ bond order = 1, F₂ ⁺ bond order = 1.5, F₂ ⁻ bond order = 0.five, strongest bond is F₂ ⁺; (e) Due north_ii bond order = iii, Northward₂ ⁺ bond gild = 2.v, Due north₂ ⁻ bail order = 2.5, strongest bond is N_ii

12. (a) H₂; (b) N_ii; (c) O; (d) C₂; (eastward) B₂

xiv. Aye, fluorine is a smaller atom than Li, so atoms in the 2s orbital are closer to the nucleus and more stable.

xvi. ii+

18. N₂ has southward-p mixing, and so the π orbitals are the last filled in North₂ ²⁺. O₂ does not have s-p mixing, then the σ _p orbital fills before the π orbitals.

Source: https://opentextbc.ca/chemistry/chapter/8-4-molecular-orbital-theory/

Posted by: welcomebusequithe.blogspot.com

Share this post